Subtract initial velocity from the final velocity: Δv = v2 - v1. Step 3: Determine Time Interval (Δt) Record the time taken for this change in velocity to occur, usually measured in seconds. Step 4:Calculate Acceleration (a) Apply the formula: Acceleration (a) = Δv / Δt. 4.. Velocity Equation in these calculations: Final velocity (v) of an object equals initial velocity (u) of that object plus acceleration (a) of the object times the elapsed time (t) from u to v. v = u + at v = u + a t. Where: u = initial velocity. v = final velocity. a = acceleration. t = time.

Find position or velocity when given acceleration as a function of time

Ex Determine the Velocity Function and Acceleration Function from the

PPT Velocity and Acceleration PowerPoint Presentation, free download
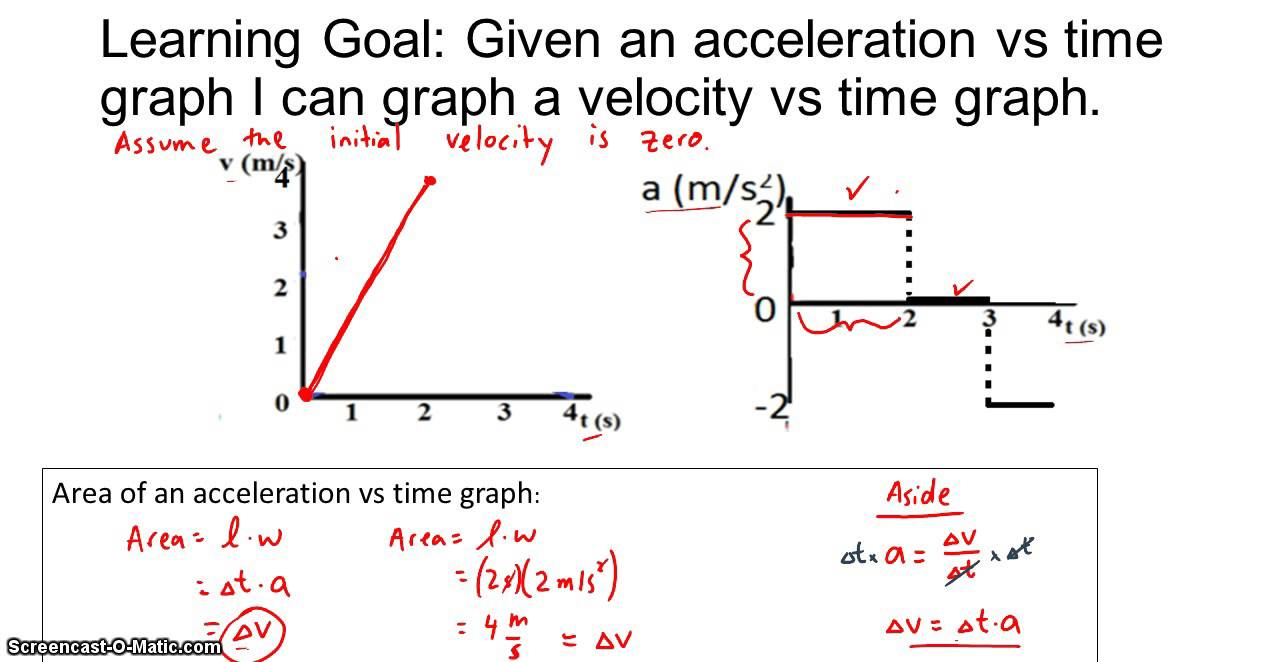
Drawing Velocity Graphs Given Acceleration Graphs YouTube

How to Find the Speed, Velocity, and Acceleration Given the Position

How To Calculate Velocity Acceleration And Distance Haiper
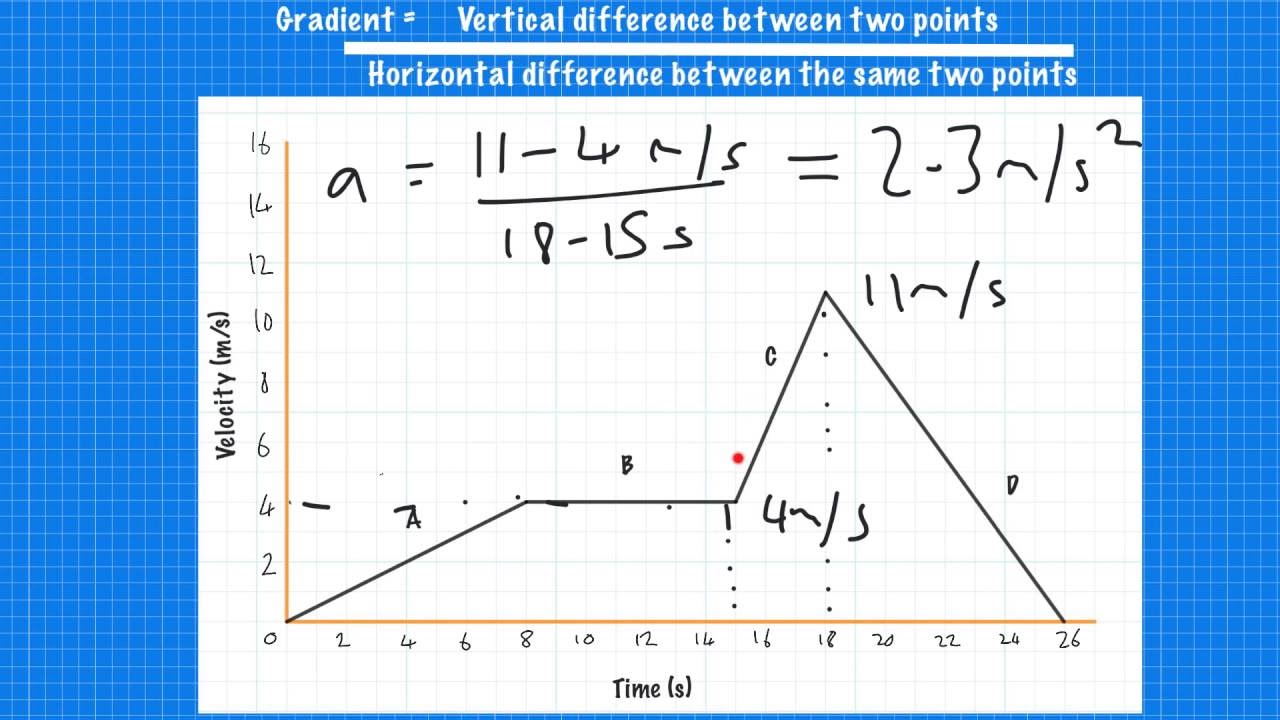
SP1d Velocity/Time Graphs Part 1 Calculating Acceleration YouTube

4 Easy Ways to Find Velocity (with Pictures) wikiHow

How to Calculate Velocity from Acceleration Data YouTube

Constant Acceleration How to Make a Velocity Graph from a Position

How To Calculate Acceleration Velocity And Time Haiper

What is Velocity? Definition, SI Unit, Examples & Applications The
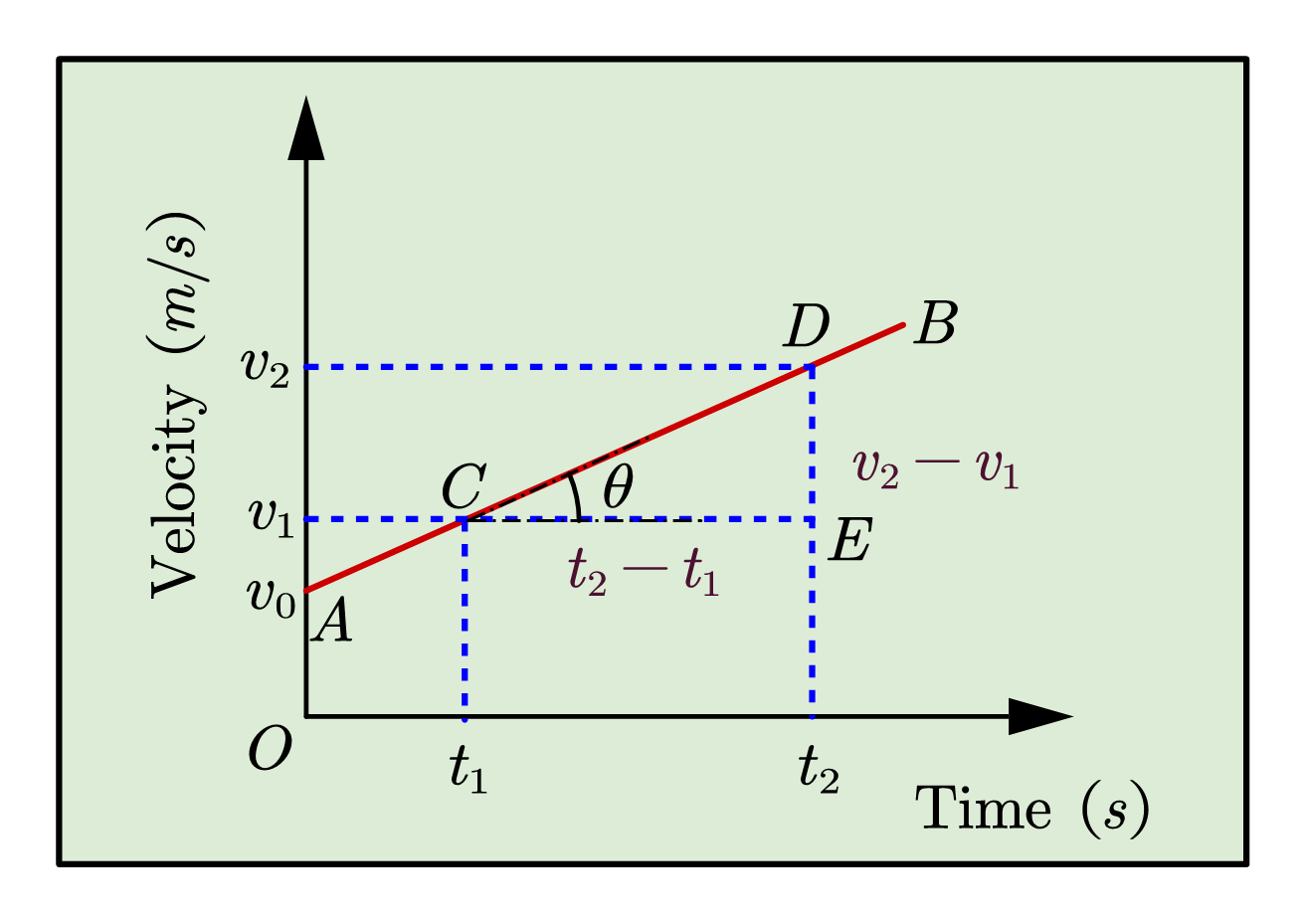
What is Velocity time graph? physicscatalyst's Blog
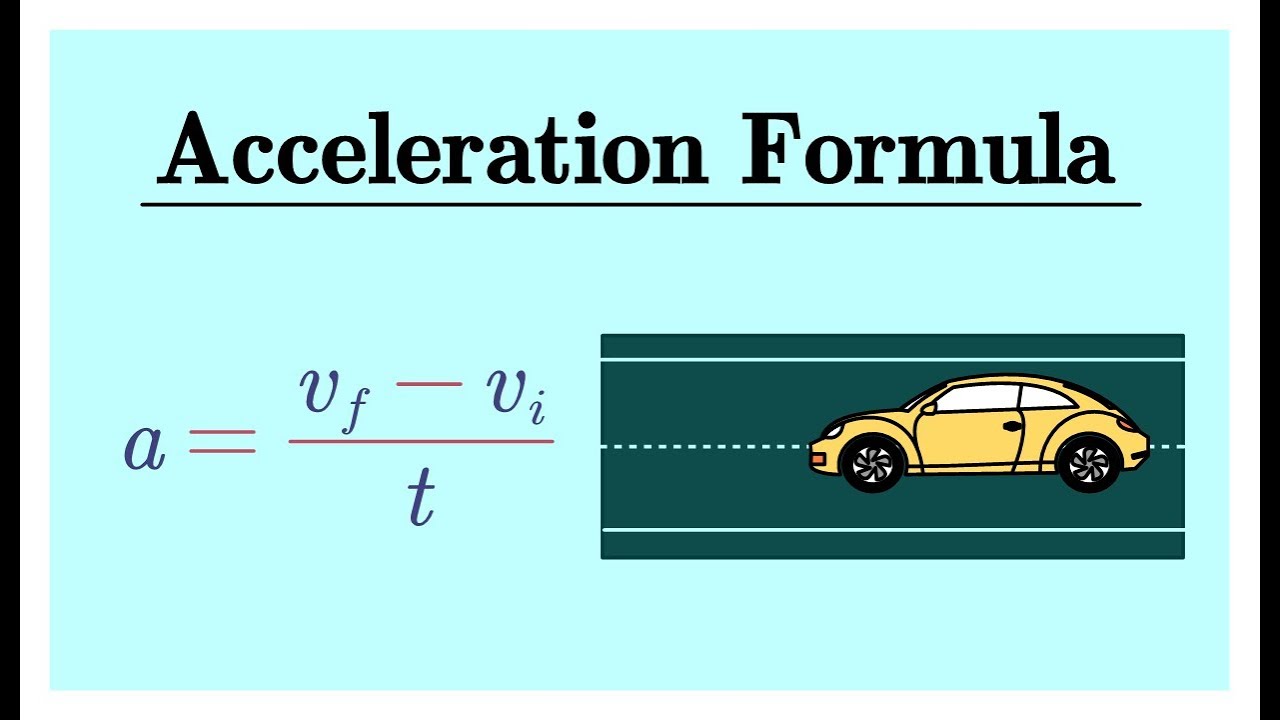
Acceleration Formula with Velocity and Time YouTube

Velocity Formula KnowItAll
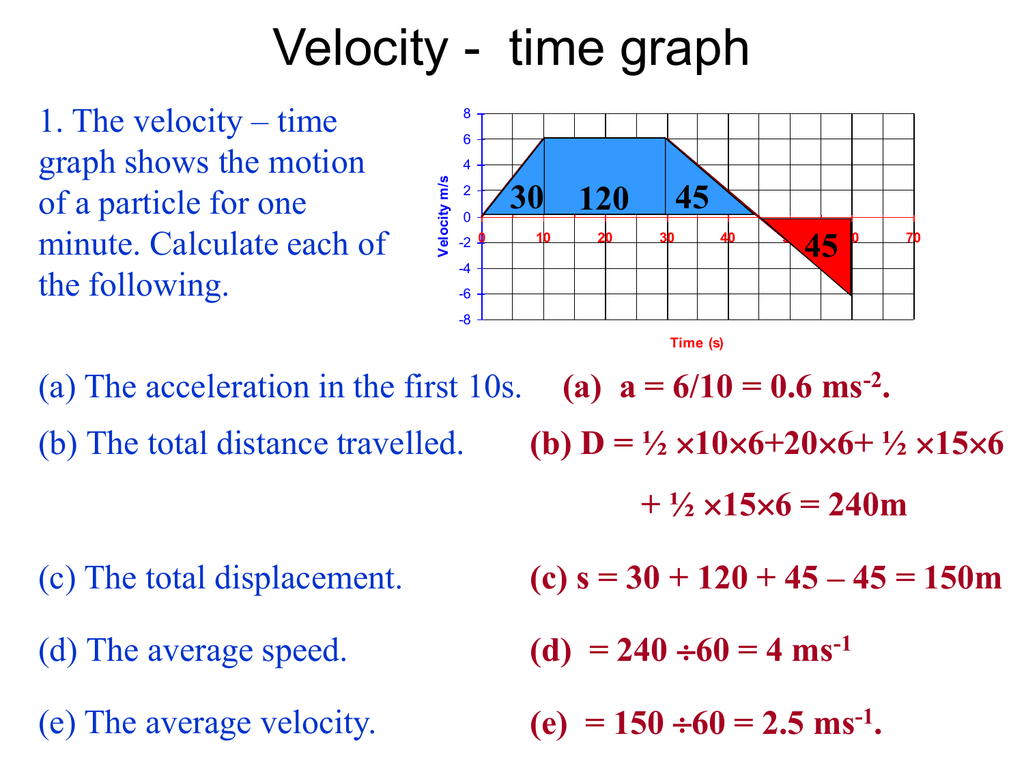
How to find acceleration on a velocity time graph 1. Velocity and

Ex Find the Velocity and Acceleration Vector Given the Position Vector

3 Ways to Calculate Acceleration wikiHow

How to Calculate Acceleration From a Velocity Time Graph Tutorial YouTube
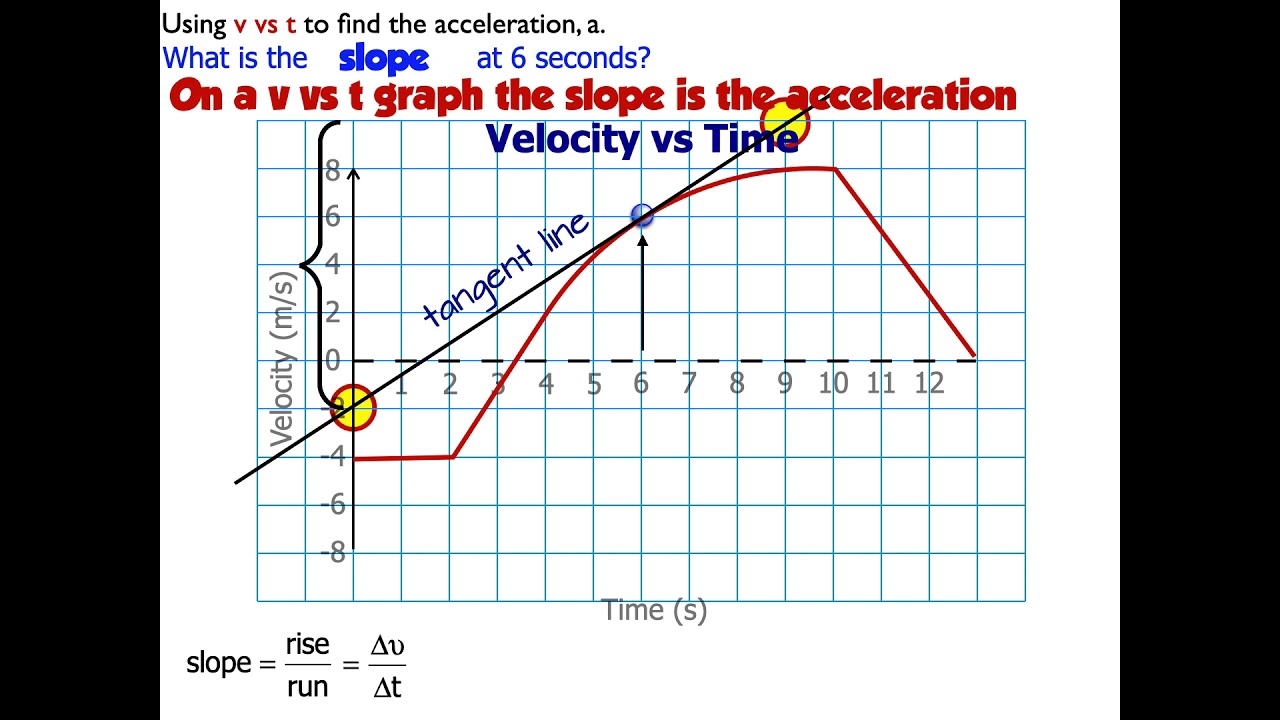
How to calculate acceleration from a velocity vs time graph YouTube
Acceleration (a) is the change in velocity (Δv) over the change in time (Δt), represented by the equation a = Δv/Δt. This allows you to measure how fast velocity changes in meters per second squared (m/s^2). Acceleration is also a vector quantity, so it includes both magnitude and direction. Created by Sal Khan.. Learn how to define and calculate the velocity and acceleration vectors of a particle moving in space using the derivative of the position function. Compare and contrast the tangential and normal components of acceleration and the perpendicularity of the velocity and acceleration vectors. Explore examples and applications of vector calculus in physics and engineering.